Pytorch 学习笔记6

本文发表于 253 天前，其中的信息可能已经事过境迁

文章摘要 TianliGPT

加载中...

本文除参考Pytorch官方文档外，还参考了为神经网络选择正确的激活函数。

通俗地讲，激活函数是一种执行计算以提供可作为下一个神经元输入的输出的函数。理想的激活函数应该使用线性概念处理非线性关系，并且应该是可微的，以减少错误并相应地调整权重。

在开始之前，我们首先来看看激活函数在哪发挥作用。这里我们以一个简单的神经网络为例，该神经网络包含一个输入层、一个隐藏层和一个输出层。

激活函数的意义

激活函数是非线性的函数，其不改变数据的尺寸，但对输入的数据值进行变换。类似人类神经元，当输入电信号达到一定程度则会激活，激活函数对于不同大小的输入，输出值应当可体现激活和抑制的区别，以此来模拟人类神经元的激活过程。

常见的激活函数

激活函数是神经网络的核心组件之一，它们是神经网络的非线性部分。激活函数的作用是将输入信号转换为输出信号。激活函数的主要目的是引入非线性性，使神经网络能够学习复杂的模式。以下是一些常见的激活函数：

ReLU

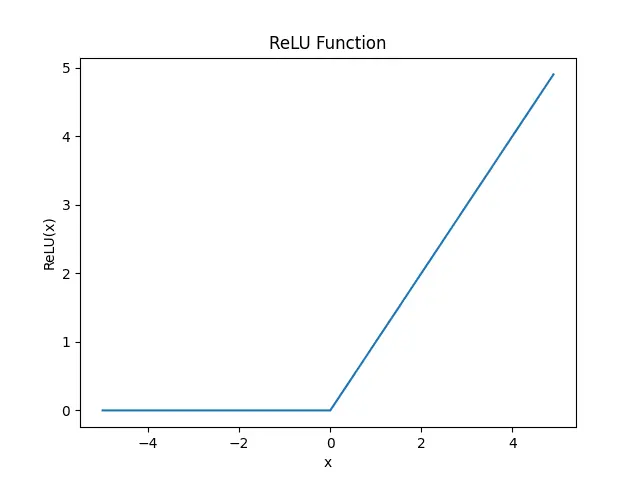
ReLU（Rectified Linear Unit）是一种非常简单的激活函数，它将所有负值都转换为零。ReLU函数的数学表达式如下：

f (x) = m a x (0, x)

我们调用pytorch中的ReLU函数来实现ReLU激活函数，并绘制其二维坐标轴中的图像。

python

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 创建一个输入张量
x = torch.arange(-5, 5, 0.1)

# 创建一个ReLU激活函数
relu = nn.ReLU()

# 计算ReLU激活函数的输出
y = relu(x)

# 绘制ReLU激活函数的图像
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('ReLU(x)')
plt.title('ReLU Function')
plt.show()

坐标系中的ReLU函数如下图所示：

ReLU函数图

ReLU 是一种流行的激活函数，因为它是可微分的和非线性的。如果输入为负，其导数将变为零，这会导致神经元“死亡”，学习不会发生。

但是，ReLU 也有一些缺点。例如，当输入为负时，ReLU 的梯度为零，这可能会导致梯度消失问题。为了解决这个问题，可以使用 Leaky ReLU 或 PReLU。

特点：

ReLU函数的发明是深度学习领域的重大突破，可以加速模型的训练过程。
ReLU函数是一个非线性函数，可以解决线性模型无法解决的问题。
ReLU函数的计算速度快，只需要判断输入是否大于0。
ReLU函数存在梯度消失问题，当输入值小于0时，梯度为0，权重无法更新。
ReLU函数输出值不是以0为中心的，可能导致梯度更新不稳定。
ReLU 函数由两个线性分量组成。因此，ReLU 函数是一个分段线性函数。所以ReLU 函数是一个非线性函数。
ReLU 函数的输出值范围是[0, +∞]，输出值不是以0为中心的，可能导致梯度更新不稳定。

用途：

ReLU 函数是MLP 和 CNN 神经网络模型中隐藏层的默认激活函数。
我们通常不会在 RNN 模型的隐藏层中使用 ReLU 函数。相反，我们在那里使用 sigmoid 或 tanh 函数。
我们从不在输出层使用 ReLU 函数。
ReLU 函数在深度学习模型中的性能非常好，因为它可以加速模型的训练过程。

Leaky ReLU

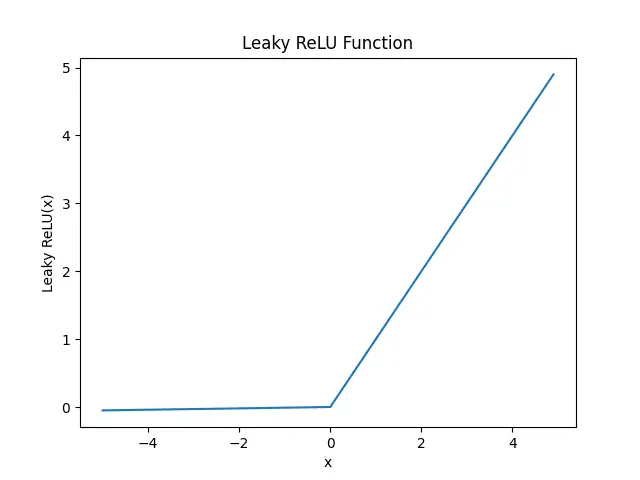
Leaky ReLU 是对 ReLU 的改进，它允许负值的梯度不为零。Leaky ReLU 的数学表达式如下：

f (x) = {\begin{cases} x, & if x > 0 \\ 0.01 x, & otherwise \end{cases}

我们调用pytorch中的LeakyReLU函数来实现Leaky ReLU激活函数，并绘制其二维坐标轴中的图像。

python

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 创建一个输入张量
x = torch.arange(-5, 5, 0.1)

# 创建一个Leaky ReLU激活函数
leaky_relu = nn.LeakyReLU(0.01)

# 计算Leaky ReLU激活函数的输出
y = leaky_relu(x)

# 绘制Leaky ReLU激活函数的图像
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('Leaky ReLU(x)')
plt.title('Leaky ReLU Function')

plt.show()

Leaky ReLU

Leaky ReLU 的主要优点是它可以避免梯度消失问题。但是，Leaky ReLU 也有一些缺点，例如它可能会导致梯度爆炸问题。

特点：

Leaky ReLU 函数是 ReLU 函数的改进版本，可以避免梯度消失问题。
Leaky ReLU 函数是一个非线性函数，可以解决线性模型无法解决的问题。
Leaky ReLU 函数的计算速度快，只需要判断输入是否大于0。
Leaky ReLU 函数存在梯度消失问题，当输入值小于0时，梯度不为0，权重可以更新。
使用leaky ReLU 的学习过程比默认的 ReLU 更快。

用途：

与 ReLU 函数一致。

Sigmoid

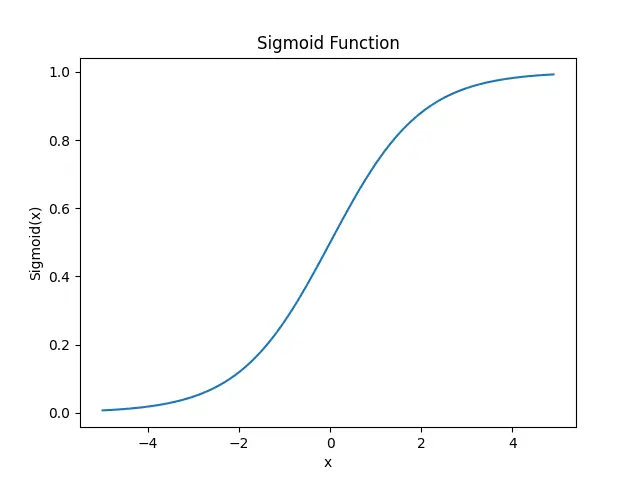
Sigmoid 是一种常用的激活函数，它将输入值转换为 0 到 1 之间的值。Sigmoid 函数的数学表达式如下：

f (x) = \frac{1}{1 + e^{- x}}

我们调用pytorch中的Sigmoid函数来实现Sigmoid激活函数，并绘制其二维坐标轴中的图像。

python

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 创建一个输入张量
x = torch.arange(-5, 5, 0.1)

# 创建一个Sigmoid激活函数
sigmoid = nn.Sigmoid()

# 计算Sigmoid激活函数的输出
y = sigmoid(x)

# 绘制Sigmoid激活函数的图像
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('Sigmoid(x)')
plt.title('Sigmoid Function')
plt.show()

Sigmoid

Sigmoid 函数的主要优点是它可以将输入值映射到 0 到 1 之间，这使得它适用于二元分类问题。但是，Sigmoid 函数也有一些缺点，例如它可能会导致梯度消失问题。因为大量输入被输入到神经网络，并且隐藏层的数量增加，梯度或导数变得接近于零，从而导致神经网络不准确。

特点：

类S型函数，输出值范围在0到1之间，可以用作二分类问题的输出层激活函数。
非线性函数，可以解决线性模型无法解决的问题。
容易导致梯度消失，当输入值较大或较小时，梯度接近于0，导致权重无法更新。
对于输入0返回0.5，输出值不是以0为中心的，可以决定给定的输入属于什么类型的两个类。
计算复杂度高，计算指数运算，计算量大。

用途：

早期被用于MLP、CNN等模型的隐藏层激活函数。
构建二进制分类模型的输出层激活函数，输出被解释为类标签。

Tanh

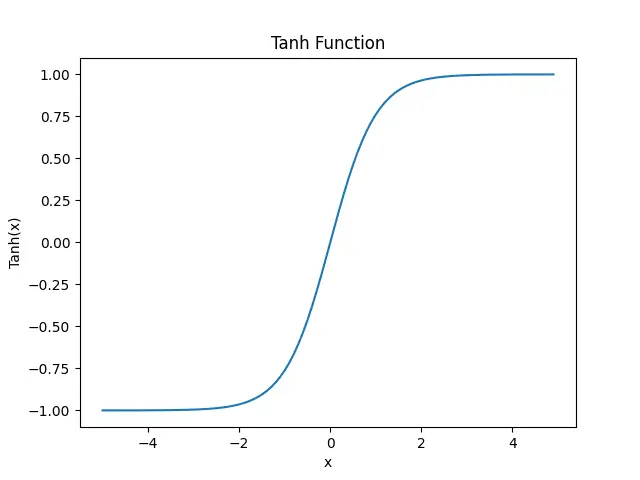
Tanh 是另一种常用的激活函数，它将输入值转换为 -1 到 1 之间的值。Tanh 函数的数学表达式如下：

f (x) = \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}

我们调用pytorch中的Tanh函数来实现Tanh激活函数，并绘制其二维坐标轴中的图像。

python

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 创建一个输入张量
x = torch.arange(-5, 5, 0.1)

# 创建一个Tanh激活函数
tanh = nn.Tanh()

# 计算Tanh激活函数的输出
y = tanh(x)

# 绘制Tanh激活函数的图像
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('Tanh(x)')
plt.title('Tanh Function')
plt.show()

Tanh

Tanh 函数的主要优点是它可以将输入值映射到 -1 到 1 之间，这使得它适用于二元分类问题。但是，Tanh 函数也有一些缺点，例如它可能会导致梯度消失问题，而且其计算较慢。

特点：

类S型函数，输出值范围在-1到1之间，可以用作二分类问题的输出层激活函数。
非线性函数，可以解决线性模型无法解决的问题。
与 sigmoid 函数相比，使用 tanh 函数的一个优点是 tanh 函数以零为中心。这使得优化过程更加容易。
比 sigmoid 函数更加陡峭，导数值更大，训练速度更快。
tanh 函数存在梯度消失问题。
计算复杂度高，计算指数运算，计算量大。

用途：

MLP、CNN等模型的隐藏层激活函数。
通常不在输出层使用tanh函数。

Softmax

Softmax 是一种常用的激活函数，它将输入值转换为 0 到 1 之间的概率分布。Softmax 函数的数学表达式如下：

f (x_{i}) = \frac{e^{x_{i}}}{\sum_{j = 1}^{n} e^{x_{j}}}

其中 $x_{i}$ 是输入向量的第 $i$ 个元素， $n$ 是输入向量的长度。

我们调用pytorch中的Softmax函数来实现Softmax激活函数，并计算其输出。

python

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 创建一个输入张量
x = torch.tensor([1.0, 2.0, 3.0])

# 创建一个Softmax激活函数
softmax = nn.Softmax(dim=0)

# 计算Softmax激活函数的输出
y = softmax(x)

# 打印Softmax激活函数的输出
print(y)

Softmax 函数的输出是一个概率分布，其所有元素的和为 1。在上面的示例中，我们创建了一个输入向量 [1.0, 2.0, 3.0]，并使用 Softmax 函数将其转换为概率分布。输出概率分布如下：

python

tensor([0.0900, 0.2447, 0.6652])

Softmax 函数的主要优点是它可以将输入值映射到 0 到 1 之间，并且所有输出值的总和为 1，这使得它适用于多类分类问题。

特点：

Softmax 函数是一个非线性函数，可以解决线性模型无法解决的问题。
Softmax 函数的输出值范围在0到1之间，所有输出值的总和为1，可以用作多分类问题的输出层激活函数。
softmax 函数计算一个事件（类）在 K 个不同事件（类）上的概率值。它计算每个类别的概率值。所有概率的总和为 1，这意味着所有事件（类）都是互斥的。

用途：

多分类问题的输出层激活函数。
通常不在隐藏层使用softmax函数。

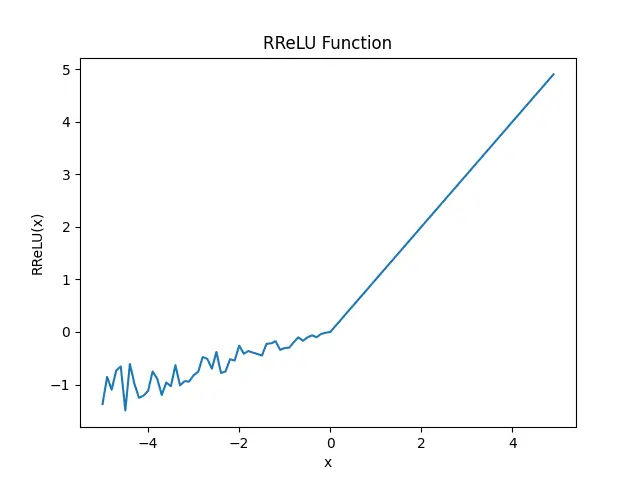
RReLU

RReLU 是对 ReLU 的改进，它引入了一个随机的负斜率。RReLU 的数学表达式如下：

f (x) = {\begin{cases} x, & if x > 0 \\ α x, & otherwise \end{cases}

其中 $α$ 是一个随机的负斜率。

我们调用pytorch中的RReLU函数来实现RReLU激活函数，并绘制其二维坐标轴中的图像。

python

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 创建一个输入张量
x = torch.arange(-5, 5, 0.1)

# 创建一个RReLU激活函数
rrelu = nn.RReLU()

# 计算RReLU激活函数的输出
y = rrelu(x)

# 绘制RReLU激活函数的图像
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('RReLU(x)')

plt.title('RReLU Function')
plt.show()

RReLU

值得注意的是，当我们调用 RReLU 函数时，它会随机生成一个负斜率。因此，每次调用 RReLU 函数时，输出都会有所不同。

RReLU 函数的主要优点是它可以避免梯度消失问题，并且引入了一个随机的负斜率，这有助于提高模型的泛化能力。

特点：

与 ReLU 函数一致

用途：

与 ReLU 函数一致。

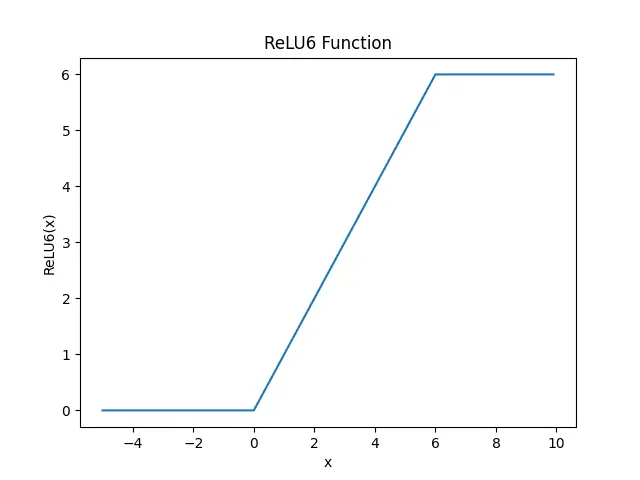
ReLU6

ReLU6 是对 ReLU 的改进，它将所有大于 6 的值都转换为 6。ReLU6 的数学表达式如下：

f (x) = min (max (0, x), 6)

我们调用pytorch中的ReLU6函数来实现ReLU6激活函数，并绘制其二维坐标轴中的图像。

python

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 创建一个输入张量
x = torch.arange(-5, 10, 0.1)

# 创建一个ReLU6激活函数
relu6 = nn.ReLU6()

# 计算ReLU6激活函数的输出
y = relu6(x)

# 绘制ReLU6激活函数的图像
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('ReLU6(x)')
plt.title('ReLU6 Function')
plt.show()

ReLU6

ReLU6 函数的主要优点是它可以将所有大于 6 的值都转换为 6，这有助于防止梯度爆炸问题。

特点：

ReLU 和 ReLU6 之间的主要区别在于，ReLU 允许正侧的值非常高，而 ReLU6 限制为正侧的值 6。任何 6 或大于 6 的输入值都将被限制为值 6（因此得名）。
ReLU6 函数由三个线性分量组成。它是一个非线性函数。

Pytorch 学习笔记6https://blog.tianli0.top/posts/2024/Pytorch6

作者Tianli

发布于2024/12/9

更新于今日内

许可协议 CC BY-NC-SA 4.0

署名-非商业性使用-相同方式共享 4.0 国际

深度学习学习笔记 Pytorch CUDA

反馈与投诉

评论隐私政策

激活函数的意义 ​

常见的激活函数 ​

ReLU ​

Leaky ReLU ​

Sigmoid ​

Tanh ​

Softmax ​

RReLU ​

ReLU6 ​

激活函数的意义

常见的激活函数

ReLU

Leaky ReLU

Sigmoid

Tanh

Softmax

RReLU

ReLU6